Equations are the lifeblood of mathematics, science, and technology. Without them, our world would not exist in its present form. However, equations have a reputation for being scary: Stephen Hawking’s publishers told him that every equation would halve the sales of A Brief History of Time.
Ignoring the advice, Hawking included E = mc² even ‘when cutting it out would have sold another 10 millions copies.” This captures our aversion to equations well. Yet, mathematician Ian Stewart argues in his book In Pursuit of the Unknown: 17 Equations That Changed the World, “[e]quations are too important to be hidden away.”
Equations are a vital part of this world. And you don’t need to be a rocket scientist to appreciate them.
There are two kinds of equations in mathematics. Stewart writes:
One kind presents relations between various mathematical quantities: the task is to prove the equation is true. The other kind provides information about an unknown quantity, and the mathematician’s task is to solve it – to make the unknown known. The distinction is not clear-cut, because sometimes the same equation can be used in both ways, but it’s a useful guideline.
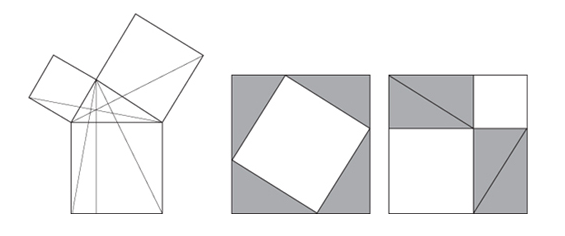
An example of the first kind of equation is Pythagoras’s theorem, which is “an equation expressed in the language of geometry.” If you accept Euclid’s basic geometric assumptions, then Pythagoras’s theorem must be true.
In the famous translation by Sir Thomas Heath, proposition 47 (Pythagoras’s theorem) of Book I reads:
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
Many triangles in real life are not right angles. But this does not limit the use of the equation a²+b² = c² because any triangle can be cut into two right-angled ones.

So understanding right-angled triangles is the key because “they prove that there is a useful relation between the shape of a triangle and the lengths of its sides.”
A good example of the second kind of equation is Newton’s law of gravity. “It tells us how the attractive force between two bodies depends on their masses,” Stewart writes, “and how far apart they are. Solving the resulting equations tells us how the planets orbit the Sun, or how to design a trajectory for a space probe.” This isn’t a mathematical theorem but rather it’s true for physical reasons in that it fits the observations.
Einstein’s general theory of relativity improves on Newton by fitting some observations better, while not messing up those where we already know Newton’s law does a good job.
Equations, as simple as they appear, have redirected human history time and time again. “An equation derives its power from a simple source,” Stewart writes, “it tells us that two calculations, which appear different, have the same answer.”
The power of equations lies in the philosophically difficult correspondence between mathematics, a collective creation of human minds, and an external physical reality. Equations model deep patterns in the outside world. By learning to value equations, and to read the stories they tell, we can uncover vital features of the world around us. This is the story of the ascent of humanity, told in 17 equations.
Pythagoras’s theorem
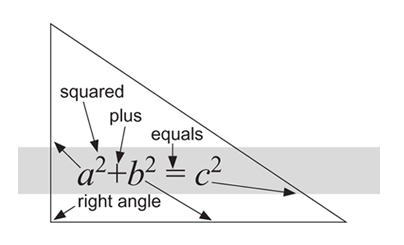
The first equation presented in the book.
What does it tell us?
How the three sides of a right-angled triangle are related.
Why is that important?
It provides a vital link between geometry and algebra, allowing us to calculate distances in terms of coordinates. It also inspired trigonometry.
What did it lead to?
Surveying, navigation, and more recently special and general relativity – the best current theories of space, time, and gravity.
History.
The Greeks did not express Pythagoras’s theorem as an equation in the modern symbolic sense. That came later with the development of algebra. In ancient times, the theorem was expressed verbally and geometrically. It attained its most polished form, and its first recorded proof, in the writings of Euclid of Alexandria. Around 250 BC Euclid became the first modern mathematician when he wrote his famous Elements, the most influential mathematical textbook ever. Euclid turned geometry into logic by making his basic assumptions explicit and invoking them to give systematic proofs for all of his theorems. He built a conceptual tower whose foundations were points, lines, and circles, and whose pinnacle was the existence of precisely five regular solids.
…
For the purposes of higher mathematics, the Greeks worked with lines and areas instead of numbers. So Pythagoras and his Greek successors would decode the theorem as an equality of areas: ‘The area of a square constructed using the longest side of a right-angled triangle is the sum of the areas of the squares formed from the other two sides.’
Maps
Surveying began to take off in 1533 when the Dutch mapmaker Gemma Frisius explained how to use trigonometry to produce accurate maps, in Libellus de Locorum Describendorum Ratione (‘Booklet Concerning a Way of Describing Places’). Word of the method spread across Europe, reaching the ears of the Danish nobleman and astronomer Tycho Brahe. In 1579 Tycho used it to make an accurate map of Hven, the island where his observatory was located. By 1615 the Dutch mathematician Willebrord Snellius (Snel van Royen) had developed the method into essentially its modern form: triangulation. The area being surveyed is covered with a network of triangles. By measuring one initial length very carefully, and many angles, the locations of the corners of the triangle, and hence any interesting features within them, can be calculated. Snellius worked out the distance between two Dutch towns, Alkmaar and Bergen op Zoom, using a network of 33 triangles. He chose these towns because they lay on the same line of longitude and were exactly one degree of arc apart.Knowing the distance between them, he could work out the size of the Earth, which he published in his Eratosthenes Batavus (‘The Dutch Eratosthenes’) in 1617. His result is accurate to within 4%. He also modified the equations of trigonometry to reflect the spherical nature of the Earth’s surface, an important step towards effective navigation.
Triangulation is an indirect way of determining distance by employing angles.
When surveying a stretch of land, be it a building site or a country, the main practical consideration is that it is much easier to measure angles than it is to measure distances. Triangulation lets us measure a few distances and lots of angles; then everything else follows from the trigonometric equations. The method begins by setting out one line between two points, called the baseline, and measuring its length directly to very high accuracy. Then we choose a prominent point in the landscape that is visible from both ends of the baseline, and measure the angle from the baseline to that point, at both ends of the baseline. Now we have a triangle, and we know one side of it and two angles, which fix its shape and size. We can then use trigonometry to work out the other two sides.
In effect, we now have two more baselines: the newly calculated sides of the triangle. From those, we can measure angles to other, more distant points. Continue this process to create a network of triangles that covers the area being surveyed. Within each triangle, observe the angles to all noteworthy features – church towers, crossroads, and so on. The same trigonometric trick pinpoints their precise locations. As a final twist, the accuracy of the entire survey can be checked by measuring one of the final sides directly.
Surveys routinely employed triangulation by the late 18th century. And while we don’t explicitly use it today, it is still there in how we deduce locations from satellite data.
In Pursuit of the Unknown: 17 Equations That Changed the World is an elegant argument for why equations matter.
